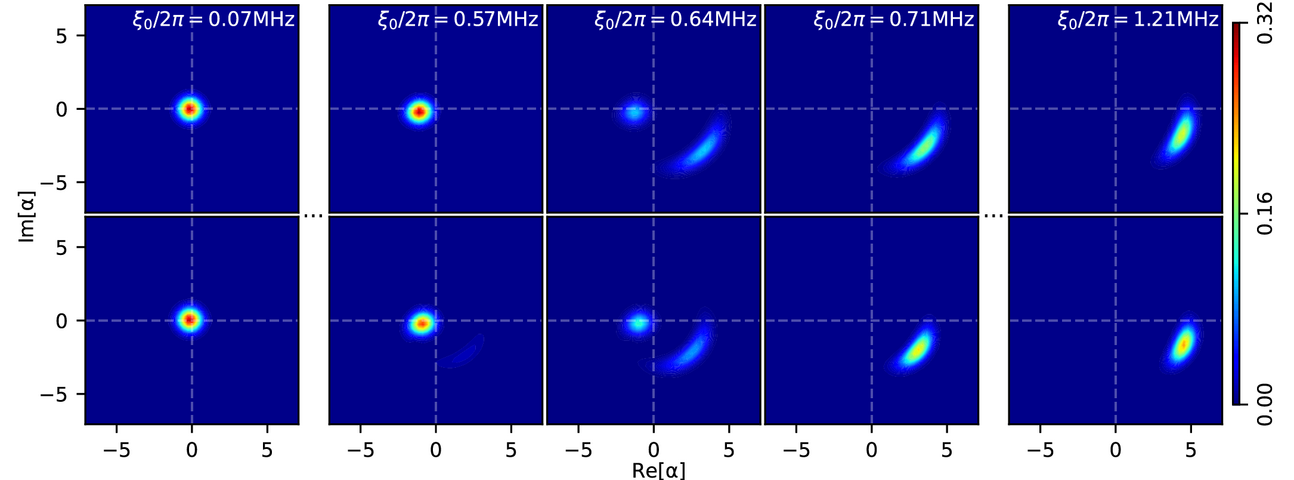
The Duffing oscillator, named after the German engineer Georg Duffing, is a simple but prototypical model system in nonlinear physics. It was stated already in 1976 by Landau and Lifshitz in their famous textbook on Theoretical Physics [1] that a remarkable feature of the Duffing oscillator is the existence of a double-well potential, leading to two steady-state solutions at the same parameter setting. This gives rise to hysteretic behavior of the oscillation amplitude as a function of the driving strength. Depending on whether one is entering the hysteretic regime on increasing or decreasing the driving strength, the Duffing oscillator assumes two different oscillation amplitudes at the same drive. This bistability of the Duffing oscillator has been extensively studied with different experimental platforms. For example, groud-breaking experiments have been performed by Gerhard Rempe et al. on optical bistability [2]. A puzzling feature, which has been addressed by Drummond and Walls already in the 1980s [3] and keeps physicists busy since then, is the fact that in contrast to the classical description a fully quantum mechanical treatment of the Duffing oscillator predicts only a single unique steady state solution and therefore no bistability [3].
As reported now in Nature Communications, a team at the Walther-Meißner-Institute (WMI) led by Prof. Gross succeeded to resolve the discrepancy. They used tunable nonlinear superconducting resonators to simulate the non-equilibrium dynamics of the Duffing oscillator. Most importantly, they succeeded to reconcile both the classical and quantum descriptions in a unified picture of quantum metastability. They revealed that the two classically regarded steady states are in fact metastable states. These states are approximate solutions of the Schrödinger equation with a remarkably long lifetime, but should eventually relax into the unique steady state predicted by quantum mechanics. By engineering the lifetime of the metastable states, they successfully observed a first-order dissipative phase transition that lies behind the intriguing behavior of the Duffing oscillator. They also performed quantum state tomography, allowing them to reveal the microscopic picture of the phase transition.
Engineered solid-state quantum systems have a huge potential
The work presented in Nature Communications is a nice example on how engineered quantum systems can be used to resolve interesting physical questions. “In general, such well-controlled, engineered solid-state quantum circuits have a huge potential both for studying important questions in basic science and for realizing applications in quantum technology”, Rudolf Gross, scientific director at WMI, professor at TUM and spokesperson of the Excellence Cluster MCQST, points out. For example, his team plans to couple several superconducting Duffing oscillators to more complex systems, allowing to perform simulations of strongly correlated bosonic systems. The general vision is to use in-situ tunable superconducting quantum circuits as a versatile platform for simulating and understanding complex problems in condensed matter physics.
[1] L. D. Landau and E. M. Lifshitz. Mechanics, volume 1 of Course of Theoretical Physics Series. Butterworth-Heinemann, 3rd edition, 1976.
[2] G. Rempe, R. J. Thompson, R. J. Brecha, W. D. Lee, and H. J. Kimble. Optical bistability and photon statistics in cavity quantum electrodynamics. Phys. Rev. Lett. 67, 1727–1730 (1991).
[3] P. D. Drummond and D. F. Walls. Quantum theory of optical bistability. I. nonlinear polarisability model. J. Phys. A: Math. Gen., 13(2): 725–741 (1980).
Source: WMI website
Publication
Quantum behavior of the Duffing oscillator at the dissipative phase transition
Q. Chen, M. Fischer, Y. Nojiri, M. Renger, E. Xie, M. Partanen, S. Pogorzalek, K. G. Fedorov, A. Marx, F. Deppe, R. Gross,
Nature Communications 14, 2896 (2023)
DOI: 10.1038/s41467-023-38217-x
Acknowledgements:
This work is funded by the German Research Foundation via Germany’s Excellence Strategy (EXC-2111-390814868), the European Union via the Quantum Flagship project QMiCS (No. 820505), and the German Federal Ministry of Education and Research via the project QuaRaTe (No. 13N15380). This research is also part of the Munich Quantum Valley, which is supported by the Bavarian state government with funds from the Hightech Agenda Bayern Plus.
Contact:
Prof. Dr. Rudolf Gross
Department of Physics, Technical University of Munich, and
Walther-Meißner-Institute, Bavarian Academy of Sciences and Humanities
Walther-Meißner-Str. 8, 85748 Garching, Germany
Phone: +49 89 289 14249, E-Mail: Rudolf.Gross(at)wmi.badw.de
Links:
- Munich Center for Quantum Science and Technology (MCQST): https://www.mcqst.de
- Munich Quantum Valley: https://www.munich-quantum-valley.de/
- EU Quantum Flagship Projekt QMiCS: https://qmics.wmi.badw.de
- WMI: https://www.wmi.badw.de
- BAdW: https://badw.de